算法裁判下间接证明的模型应用——基于类案证据环的构建

　　内容摘要：深度学习的计算机语言实现类案检索智能化、校验判断自主化、文件生成自动化等初级司法人工智能，计算机规则模型及算法裁判或将成为高级司法人工智能的最终形态。间接证明运行中，间接证据-间接事实-主要事实的认定过程与人工智能运行逻辑存在内生契合。以证据链、证据环和复合型证据环为基础模型，通过提取关键间接证据与间接事实，构建类案间接证明模型库。当复杂案件存在相悖的证据群及多个争议间接事实时，事实裁判者可在模型库中选择适用间接证明模型，在填充证据环过程中，厘清证据间的逻辑关系，修正主观预断。继而借助计算机算法，运用概率推理获得证据环上整体证据群对要件事实为真的推论概率，检验证明结论的合理性或正当性。

　　关键词：人工智能；算法裁判；间接证明；证据环；概率推理

　　一、证据环对间接证明的整体效用分析

　　证据法上将证据分为直接证据与间接证据，鉴于直接证据资源的匮乏及证明力的不稳定性，藉由间接证据先行证实间接事实，再运用经验法则推论出主要事实存在与否，是司法证明中最常用的证明方法，此即间接证明。然而间接证明至今尚未发展出完整的证明方法体系，证成活动缺乏内部逻辑的客观化展示，难以证立结论的正当性或合理性。实证研究发现，事实裁判者运用间接证明认定要件事实时，证据评价缺失、证明链条断裂、逻辑推论模糊、证明结论偏离在间接证明过程中逐次发生，心证过程“神秘化”，证成活动缺乏客观展示，间接证明的最终推定力备受质疑。

　　间接证明过程中，间接证据-间接事实-主要事实的法律推理与人工智能的形式逻辑存在内生契合，具备智能化的可操作性。计算机精密明确的规则模型，能够从多维角度观测待证事实，为各方事实博弈搭建可观测的相互作用的指令结构，为探寻算法裁判提供理性科学的路径。搭建证据环规则模型，链接全案间接证据，形成稳定、可检验的证明结构，能有效检视证据链条的完整性，审查判断复杂证据群，完成全案证据的逻辑排列，揭示证成活动的内部推论结构，展现证据与要件事实之间的逻辑关系。

　　二、间接证明闭合证据环的三重递进构建

　　间接证明过程因缺乏系统的证明方法的规制与指导，以至于事实认定“始终处于威格莫尔所说的那种令人不解的、缺乏指导的以及不稳定的状态”。证据环是所有证据组成的、环环相扣的、能够客观还原案件事实的证据联结结构。将一般的间接证明过程提炼为抽象思维模式，具体可分为三种情形，即证据链、证据环和复合型证据环。

　　证据链是利用间接证据证明间接事实，再运用经验法则推论出主要事实，即“间接证据-间接事实-主要事实”的证明运行模式。

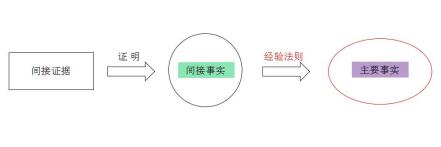
　　图1：证据链模型

　　证据环是以单数或复数的间接证据证明间接事实，再以多个间接事实联合的方式证明主要事实的证明运行模式。

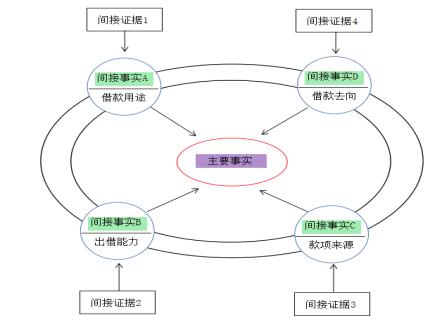
　　图2：证据环模型

　　复合型证据环即同时使用证据链与证据环，运用不同的证明方式推论出不同的间接事实，集合不同间接事实推论出其他间接事实，最终推导出主要事实的证明运行模式。运用复合型证据环，提取关键性间接事实时，应结合个案间接证据及争议焦点的不同情况作出适当调整，实现“事实认定符合客观真相”的证明目标。

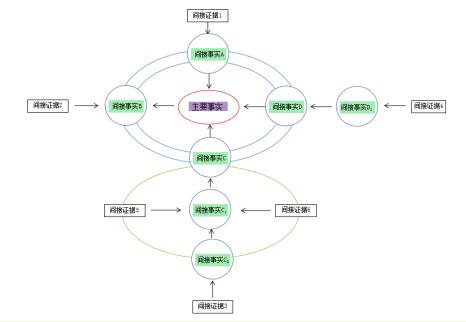
　　图3：复合型证据环模型

　　以全案间接证据构建证据链、证据环、复合型证据环的间接证明模型，将证据与事实予以“链接”，证据之间以及证据与事实之间的交流和互动生动直观，内化在双方当事人和法官内心的抽象推论步骤借助于此模型均清晰的予以表达。同时，事实裁判者的主观预断会在模型构建中反复修正，裁判的理性得以实现。

　　三、间接证明中证据价值的赋值区间与概率推理

　　间接证明的规范适用，除依靠间接证明模型这一客观化介质外，尚需“概率性进路”的建立。引入计算机算法精确化处理与表达证据信息，以客观数值证立结论的合理性，裁判过程数据化表达。

　　（一）赋值区间与量化计算

　　证据环本质上是对间接证据整体证据价值的盖然性衡量。有学者认为，当复杂的推论问题涉及不确定性作为典型特征需要以一种连贯的方式捕获与处理时，正是使用概率的标准框架，它的清晰表达与彻底的计算架构能够提供非常有助益的帮助。概率推理通过条件化概率搭建推理链接继而形成复杂的概率决策网络，结合传统数学公理和贝叶斯定理即可获得单项或多项证据对要件事实的推论力量，最终确定该要件事实是否最有可能发生。

　　根据证据的证明力强弱，可以将间接证据单独证成某一间接事实的可信性划分为五个等级，即完全盖然性、高度盖然性、较高盖然性、一般盖然性及较低盖然性，并对每个等级的证成概率自50%至100%进行区间划分（见表1）。

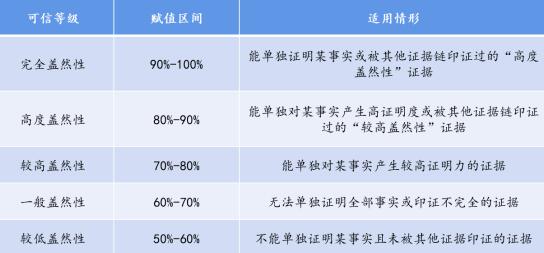
　　表1：证明力等级表

　　在证据链中，各间接证据处于同等级，且均为证成同一事实，该证据链的整体证明力即为各间接证据盖然性相乘之结果。举例言之，以间接证据A推断间接事实B的盖然性为80%，以间接事实B推断主要事实C的盖然性为80%，则此证据链的抽象证明力为80%×80%=64%。

　　（二）概率推理与案例演示

　　概率推理是一种在接受新证据后更新我们关于某个假说或主张的信念程度之有效规则。证据环中，间接证据分别证成不同的间接事实；复合型证据环中，间接证据间又彼此存在一定的层级关系，最终层级的间接证据用以推论主要事实。此时，间接证据组合推论主要事实时往往存在不确定性，而概率推理旨在驯服这种不确定性。贝叶斯定理是归纳推理中关于概率演算的法则，能够对多个证据的证明力进行结合，解释证据的似然比，从而得出关于最终事实命题的后验概率。

　　首先确定初始盖然性，所谓初始盖然性乃指某一因特定间接证据所可引致对盖然性增加之前已存在之盖然性。假设100组无任何证据的民间借贷案件中，存在借贷事实的有30组，依Bayes定律，其初始盖然性为：

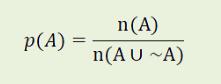
　　亦即：

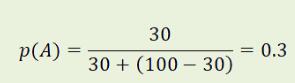
　　Bayes理论对加入间接证据后新盖然性的变化提出如下公式：

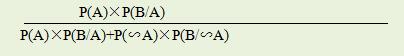
　　亦即：

　　依上述事实，假设存在借贷事实时，借款人银行账户出现明显财产变化的概率为80%【P(B/A)】,不存在借贷事实时，借款人银行账户出现明显财产变化的概率为5%【P(B/-A)】。计算出反应借款人银行账户出现明显财产变化的确有借贷事实之盖然性为：

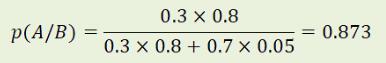
　　据此可知，加入了借款人银行账户出现明显财产变化的间接证据，其盖然性自30%增至87.3%。

　　运用概率推理时，借助大数据分析获取科学客观的先验概率，再通过计算机算法获得后验概率。概率推理可用以检验证据对事实命题的支持效果，虽然面临主观概率赋值不精确的难题，但推理规则可以通过计算机程序实现，能够提高事实裁判者在间接证明中准确认定事实的能力。

　　结语

　　司法人工智能体系建设应真正回应裁判者的实质需求。当前技术背景下，借助大数据分析与人工智能的深度融合，搭建类案计算机规则模型，从数据库中归纳出统一的证据适用标准，通过计算机算法为司法裁判提供预测参考，是司法人工智能解决实际问题的有效路径，也为算法裁判提供方法论上的启示。

　　责任编辑：广汉